【力扣】111. 二叉树的最小深度

给定一个二叉树，找出其最小深度。

最小深度是从根节点到最近叶子节点的最短路径上的节点数量。

说明：叶子节点是指没有子节点的节点。

示例 1：

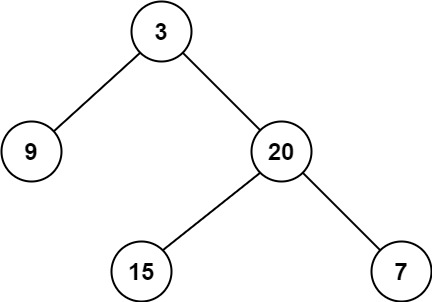
输入：root = [3,9,20,null,null,15,7]
输出：2

示例 2：

输入：root = [2,null,3,null,4,null,5,null,6]
输出：5

提示：

• 树中节点数的范围在 [0, 105] 内
• -1000 <= Node.val <= 1000

题解：

递归法（深度优先）：

// 时间复杂度：O(n)
// 空间复杂度：O(n)
func minDepth(root *TreeNode) int {
	if root == nil {
		return 0
	}
	min := func(a, b int) int {
		if a < b {
			return a
		}
		return b
	}
	if root.Left == nil && root.Right == nil {
		return 1
	}
	minD := math.MaxInt
	if root.Left != nil {
		minD = min(minDepth(root.Left), minD)
	}
	if root.Right != nil {
		minD = min(minDepth(root.Right), minD)
	}
	return minD + 1
}

使用队列解决（广度优先）：

// 时间复杂度：O(n)
// 空间复杂度：O(n)
func minDepth(root *TreeNode) int {
	if root == nil {
		return 0
	}
	minD := math.MaxInt
	depth := 1
	queue := list.New()
	queue.PushBack(root)
	for queue.Len() > 0 {
		length := queue.Len()
		for i := 0; i < length; i++ {
			node := queue.Remove(queue.Front()).(*TreeNode)
			if node.Left == nil && node.Right == nil {
				return depth
			}
			if node.Left != nil {
				queue.PushBack(node.Left)
			}
			if node.Right != nil {
				queue.PushBack(node.Right)
			}
		}
		depth++
	}
	return minD
}