【力扣】59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

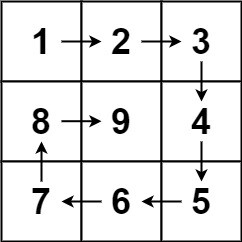
示例 1：

输入：n = 3
输出：[[1,2,3],[8,9,4],[7,6,5]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

• 1 <= n <= 20

题解：

// 时间复杂度：O(n^2)
// 空间复杂度：O(n^2)
func generateMatrix(n int) [][]int {
	// x, y 的初始位置
	startX, startY := 0, 0
	// offset 的目的在于每次循环时更新矩阵的终止位置
	offset := 1
	// 循环几圈
	loop := n >> 1
	// 中心点（奇数）的位置
	center := n >> 1
	// 记录数字的增加
	count := 1
	// 初始化一个二维切片
	res := make([][]int, n)
	for i := range res {
		res[i] = make([]int, n)
	}
	// 模拟旋转
	for loop > 0 {
		x, y := startX, startY
		// 从左上到右上 行数不变x 列数在变y++
		for ; y < n-offset; y++ {
			res[x][y] = count
			count++
		}
		// 从右上到右下 行数在变x++ 列数不变y
		for ; x < n-offset; x++ {
			res[x][y] = count
			count++
		}
		// 从右下到左下 行数不变x 列数在变y--
		for ; y > startY; y-- {
			res[x][y] = count
			count++
		}
		// 从左下到左上 行数变化x-- 列数不变y
		for ; x > startX; x-- {
			res[x][y] = count
			count++
		}
		startX++
		startY++
		offset++
		loop--
	}
	// 如果余1则代表矩阵正中心有一个坐标尚未填充，这里处理了一下
	if n%2 == 1 {
		res[center][center] = count
	}
	return res
}