【力扣】144. 二叉树的前序遍历

给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

示例 1：

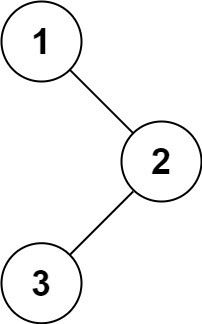
输入：root = [1,null,2,3]
输出：[1,2,3]

示例 2：

输入：root = []
输出：[]

示例 3：

输入：root = [1]
输出：[1]

示例 4：

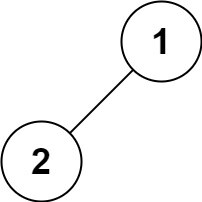
输入：root = [1,2]
输出：[1,2]

示例 5：

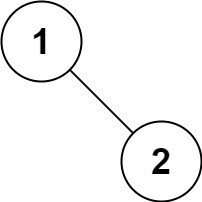
输入：root = [1,null,2]
输出：[1,2]

提示：

• 树中节点数目在范围 [0, 100] 内
• -100 <= Node.val <= 100

进阶：递归算法很简单，你可以通过迭代算法完成吗？

题解：

递归法：

// 时间复杂度：O(n)
// 空间复杂度：O(n)
func preorderTraversal(root *TreeNode) []int {
	var result []int
	var preorder func(node *TreeNode)
	preorder = func(node *TreeNode) {
		if node == nil {
			return
		}
		result = append(result, node.Val)
		preorder(node.Left)
		preorder(node.Right)
	}
	preorder(root)
	return result
}

迭代法：

// 时间复杂度：O(n)
// 空间复杂度：O(n)
func preorderTraversal(root *TreeNode) []int {
	var result []int
	if root == nil {
		return result
	}
	st := list.New()
	st.PushBack(root)
	for st.Len() > 0 {
		// 返回尾部最后一个节点并删除掉
		node := st.Remove(st.Back()).(*TreeNode)
		result = append(result, node.Val) // 中
		// 基于栈先进后出的原则，这里入栈的时候先让右节点进入再让左节点进
		// 出栈的时候优先从左节点出，再从右节点出。顺应了前序遍历的：中 左 右
		if node.Right != nil {
			st.PushBack(node.Right) // 左
		}
		if node.Left != nil {
			st.PushBack(node.Left) // 右
		}
	}
	return result
}

第二种迭代法：

// 时间复杂度：O(n)
// 空间复杂度：O(n)
func preorderTraversal(root *TreeNode) []int {
	var result []int
	// 创建一个栈 并将 root 节点压入栈
	stack := list.New()
	stack.PushBack(root)
	// 遍历二叉树各个节点
	for stack.Len() > 0 {
		// 取出并删除二叉树栈顶元素
		e := stack.Back()
		stack.Remove(e)
		// 栈顶元素如果为 nil，说明需要遍历当前节点
		if e.Value == nil {
			// 取出并删除下一个栈顶元素（当前节点）
			e = stack.Back()
			stack.Remove(e)
			node := e.Value.(*TreeNode)
			result = append(result, node.Val)
			continue
		}
		node := e.Value.(*TreeNode)
		// 如果右子树非空，将右子节点压入栈
		if node.Right != nil {
			stack.PushBack(node.Right)
		}
		// 如果左子树非空，将左子节点压入栈
		if node.Left != nil {
			stack.PushBack(node.Left)
		}
		// 压入当前节点后再压入一个 nil 做标记
		stack.PushBack(node)
		stack.PushBack(nil)
	}
	return result
}